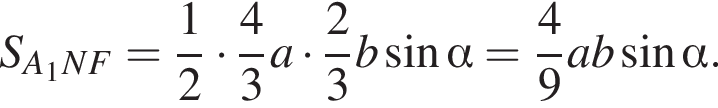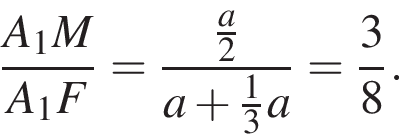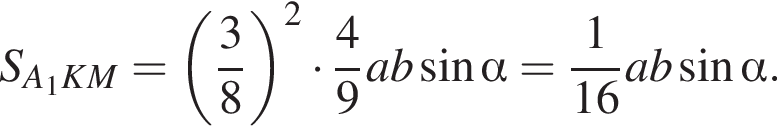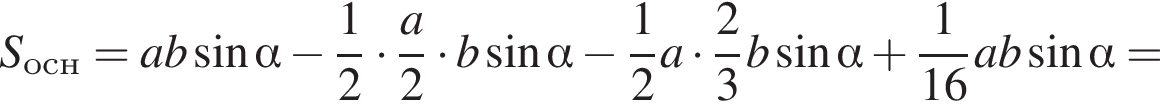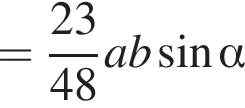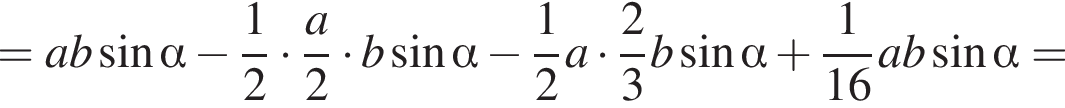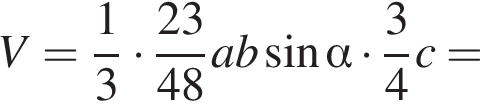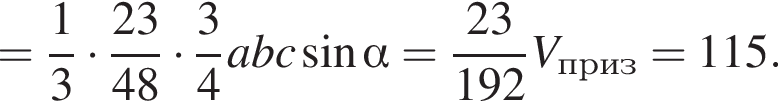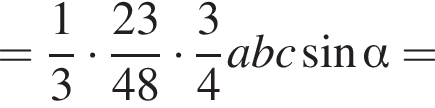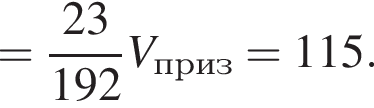На координатной прямой отмечены точки А, В, С, D, F. Числу ![]() на координатной прямой может соответствовать точка:
на координатной прямой может соответствовать точка:
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
Если 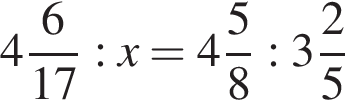 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
Даны квадратные уравнения:
Укажите уравнение, которое не имеет корней.
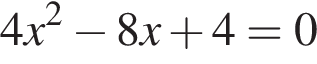
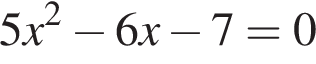
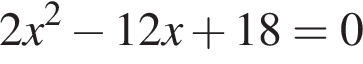
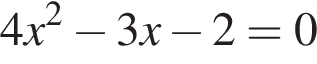
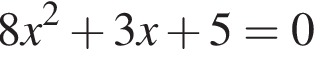
Вычислите 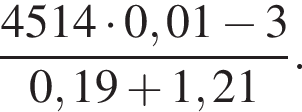
На рисунке приведен график изменения скорости тела в зависимости от времени. Запишите закон движения тела на промежутке от 40 мин до 80 мин.
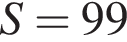

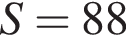
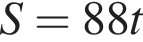

Решите неравенство 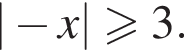
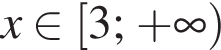

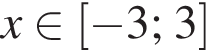
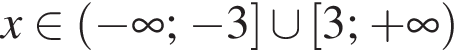
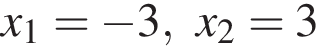
Пусть a = 3,6; b = 7,8 · 101. Найдите произведение ab и запишите его в стандартном виде.
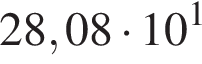
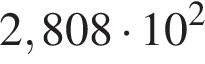
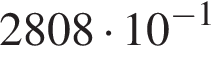

От пристани одновременно отправляются по течению реки катер(I) и против течения реки моторная лодка (II). На рисунке приведены графики их движения. Определите скорость течения реки (в км/ч), если катер и моторная ложка имеют одинаковые собственные скорости.
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
На круговой диаграмме показано распределение посевных площадей под зерновые культуры в агрохозяйстве. Сколько гектаров отведено под рожь, если пшеницей засеяно на 300 га больше, чем гречихой?
Укажите номер рисунка, на котором представлен эскиз графика функции y = 4 − (x + 1)2.
Объем конуса равен 5, а его высота равна ![]() Найдите площадь основания конуса.
Найдите площадь основания конуса.
В ботаническом саду разбили клумбу треугольной формы. Длина первой стороны клумбы равна 6 м, длина второй стороны в 2,5 раза больше длины первой, а длина третьей составляет не меньше 120% от длины второй стороны. Какому условию должен удовлетворять периметр Р (в метрах) этой клумбы.
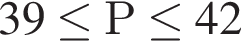
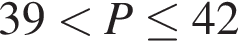


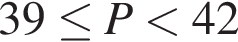
Точки A, B, C лежат на большой окружности сферы так, что треугольник ABC — равносторонний. Если AB = ![]() то площадь сферы равна:
то площадь сферы равна:
ABCDA1B1C1D1 — прямоугольный параллелепипед такой, что AB = 16, AD = 2. Через середины ребер AA1 и BB1 проведена плоскость (см.рис.), составляющая угол 60° с плоскостью основания ABCD. Найдите площадь сечения параллелепипеда этой плоскостью.
График функции, заданной формулой y = kx + b, симметричен относительно начала координат и проходит через точку A (2; 6). Значение выражения k + b равно:
Найдите наименьший положительный корень уравнения 

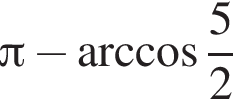
Витя купил в магазине некоторое количество тетрадей, заплатив за них 24 тысячи рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 1 тысячу рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 2 тетради больше. Сколько тетрадей купил Витя?
Выберите три верных утверждения, если известно, что прямая а перпендикулярна плоскости
![]() и пересекает ее в точке О.
и пересекает ее в точке О.
1) Любая прямая, перпендикулярная плоскости ![]() параллельна прямой а.
параллельна прямой а.
2) Любая прямая, перпендикулярная прямой а, лежит в плоскости ![]()
3) Прямая а перпендикулярна любой прямой плоскости ![]()
4) Через прямую а проходит единственная плоскость, перпендикулярная плоскости ![]()
5) Существует множество плоскостей, перпендикулярных прямой а.
6) Существует единственная прямая, параллельная прямой а и перпендикулярная плоскости ![]()
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
В двух сосудах 57 литров жидкости. Если 5% жидкости из первого сосуда перелить во второй, то в обоих сосудах окажется одинаковое количество жидкости. Сколько литров жидкости было во втором сосуде первоначально?
Найдите произведение корней (корень, если он единственный) уравнения 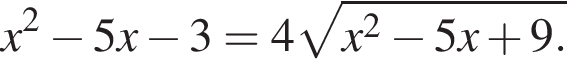
В параллелограмме с острым углом 45° точка пересения диагоналей удалена от прямых, содержащих неравные стороны, на расстояния ![]() и 2. Найдите площадь параллелограмма.
и 2. Найдите площадь параллелограмма.
Три числа составляют геометрическую прогрессию, в которой ![]() Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 32, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 32, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Функция y = f(x) определена на множестве действительных чисел ![]() является нечетной, периодической с периодом T = 26 и при
является нечетной, периодической с периодом T = 26 и при  задается формулой
задается формулой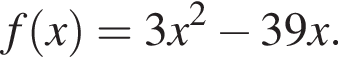 Найдите произведение абсцисс точек пересечения прямой y = 36 и графика функции y = f(x) на промежутке [ −33; 15].
Найдите произведение абсцисс точек пересечения прямой y = 36 и графика функции y = f(x) на промежутке [ −33; 15].
Найдите сумму наименьшего и наибольшего целых решений неравенства 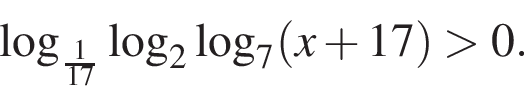
Найдите (в градусах) сумму корней уравнения  на промежутке (90°; 140°).
на промежутке (90°; 140°).
Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 1, высота пирамиды — 3. Найдите площадь S поверхности куба. В ответ запишите значение выражения 8S.
Из двух растворов с различным процентным содержанием спирта массой 300 г и 700 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
ABCDA1B1C1D1 — прямая четырехугольная призма, объем которой равен 960. Основанием призмы является параллелограмм ABCD. Точки M и N принадлежат ребрам A1D1 и С1D1, так что A1M : A1D1 = 1 : 2, D1N : NC1 = 2 : 1. Отрезки A1N и B1M пересекаются в точке K. Найдите объем пирамиды SB1KNC1, если 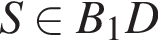 и B1S : SD = 3 : 1.
и B1S : SD = 3 : 1.

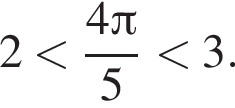 Таким образом, точка B может соответствовать этому числу.
Таким образом, точка B может соответствовать этому числу.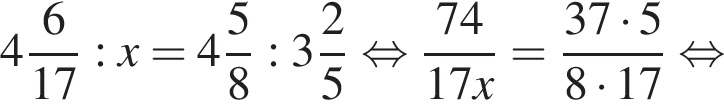
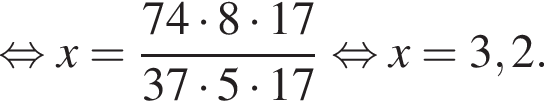
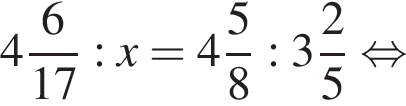
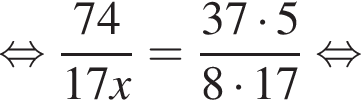
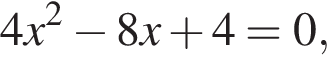 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.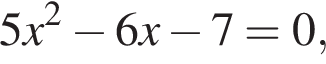 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.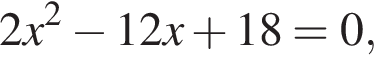 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.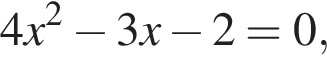 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.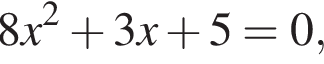 дискриминант меньше нуля, значит, корней нет.
дискриминант меньше нуля, значит, корней нет.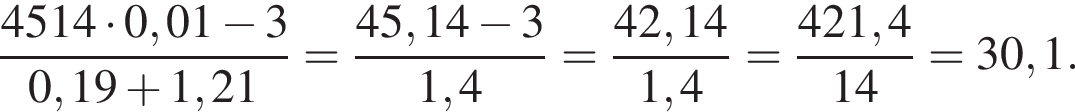
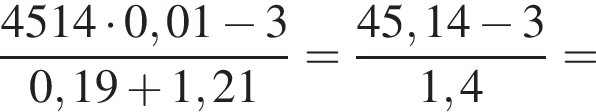
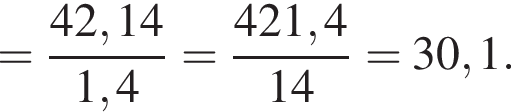


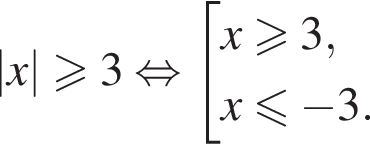
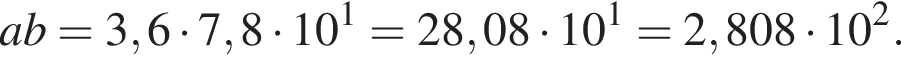
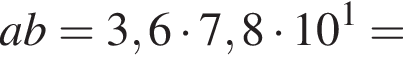
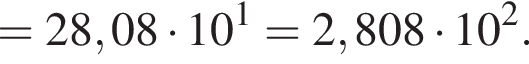
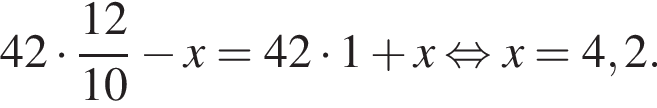

 Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная гречихой. Тогда
Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная гречихой. Тогда 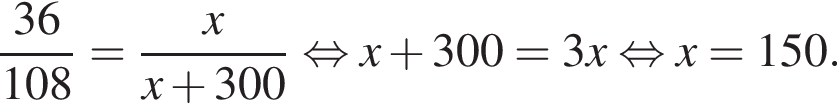
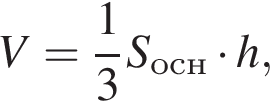 поэтому
поэтому 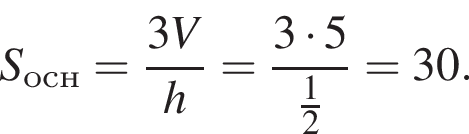
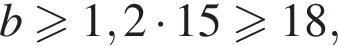 а также
а также 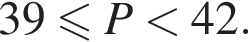
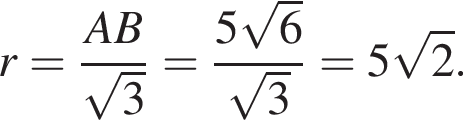 Площадь сферы равна
Площадь сферы равна 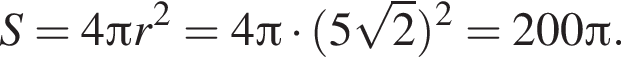

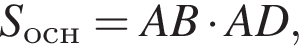 таким образом:
таким образом: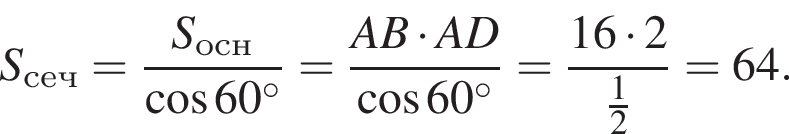
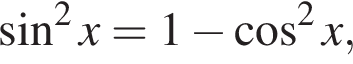 получим:
получим: 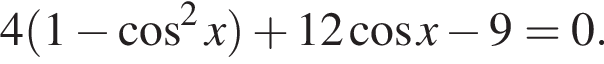 Сделаем замену
Сделаем замену 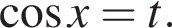 Решим уравнение:
Решим уравнение: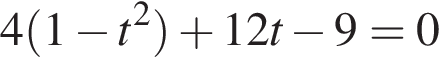
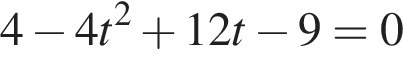
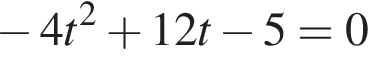
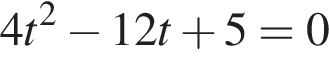
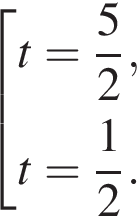
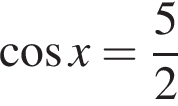 или
или 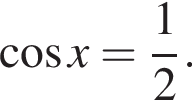 Первое уравнение решений не имеет, поскольку
Первое уравнение решений не имеет, поскольку 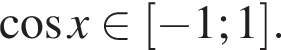 Рассмотрим второе уравнение:
Рассмотрим второе уравнение: 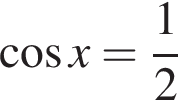
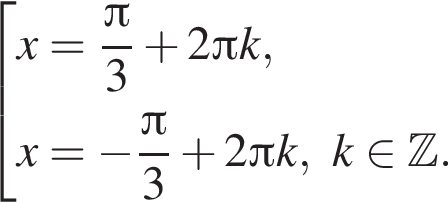
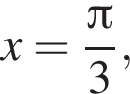 он указан под номером 3.
он указан под номером 3. Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство
Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство 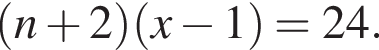 Решим систему уравнений:
Решим систему уравнений: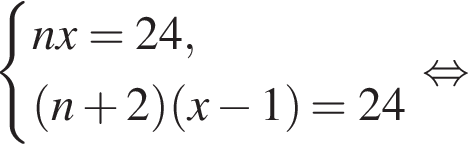
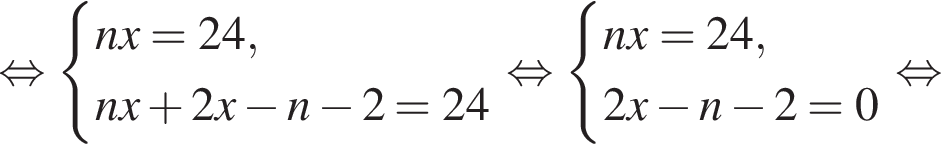
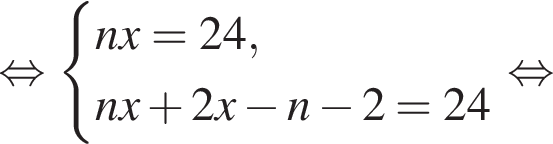
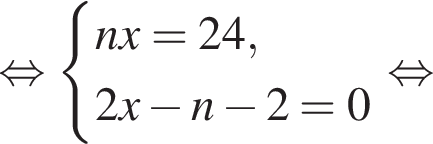
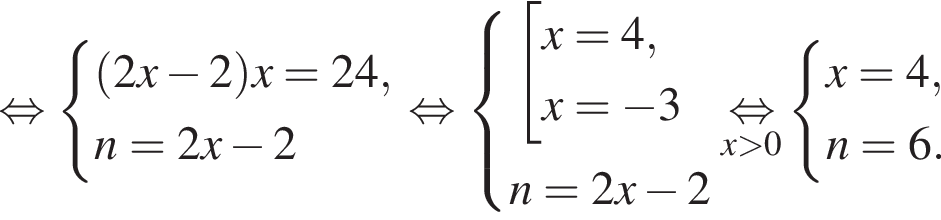
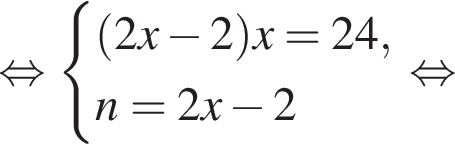
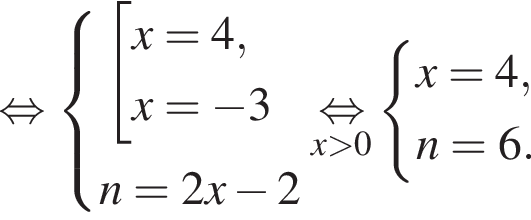
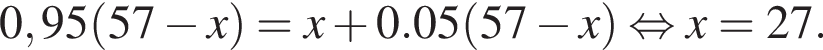


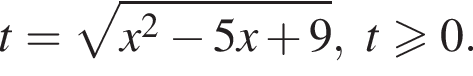 Имеем:
Имеем: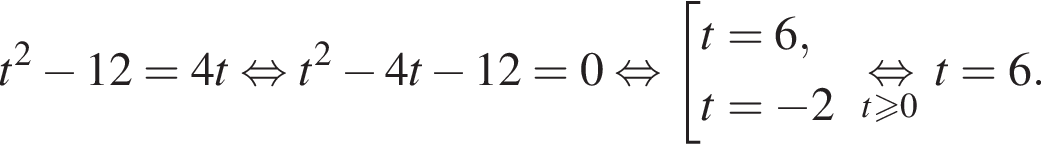
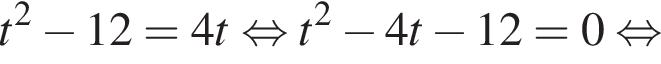
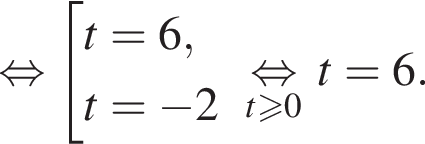

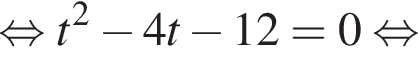
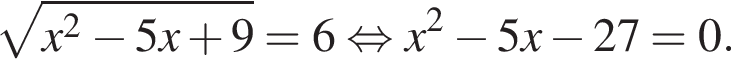 Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −27.
Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −27.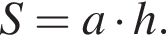 Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 2 = 4:
Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 2 = 4: 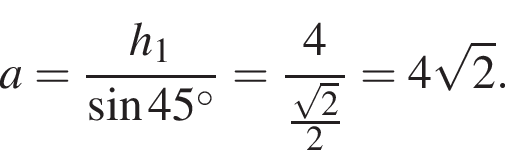 Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту
Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту 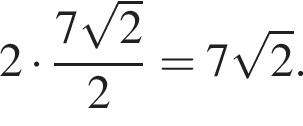
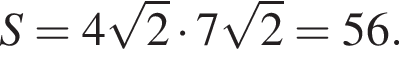
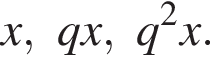
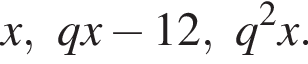
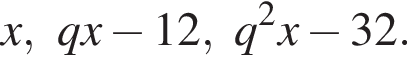
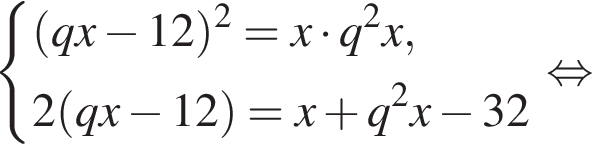
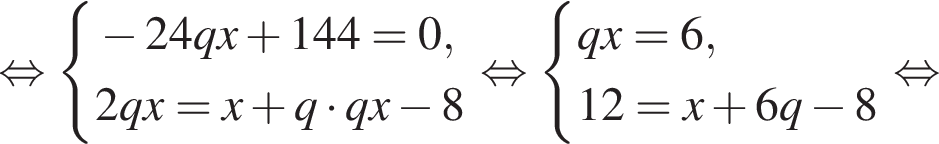
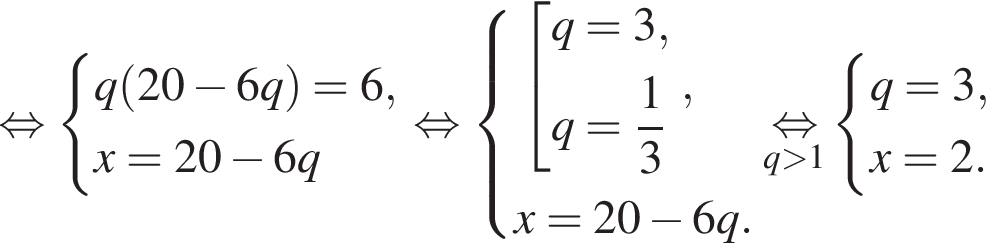
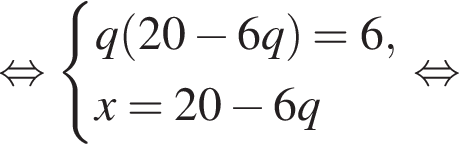
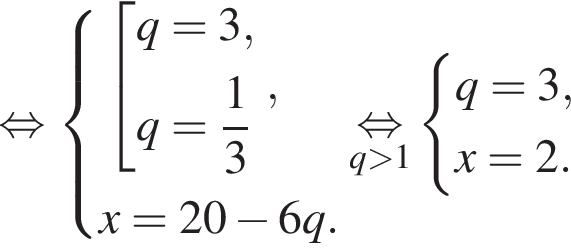
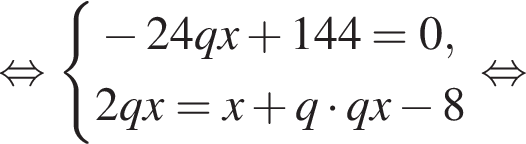
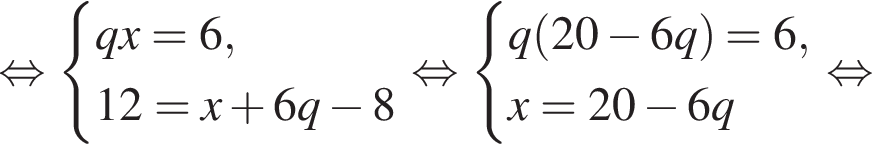
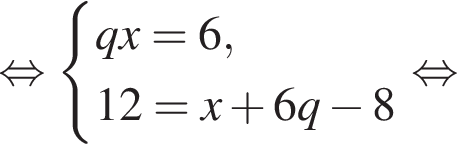
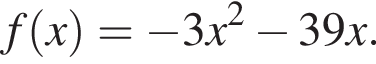 Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 36.
Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 36. 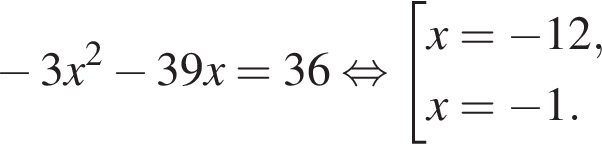

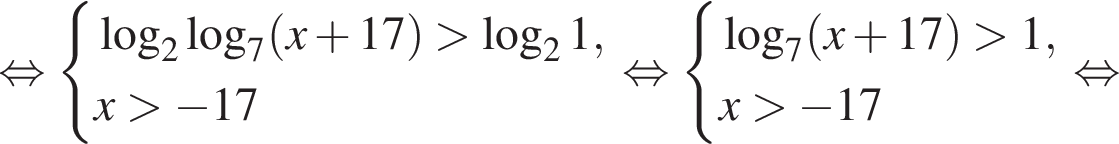
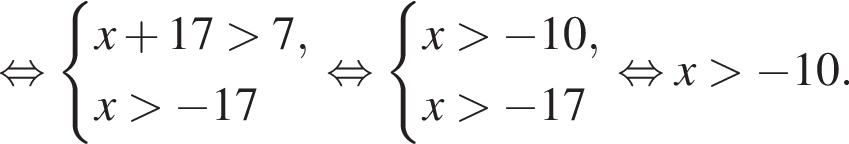
 тогда:
тогда: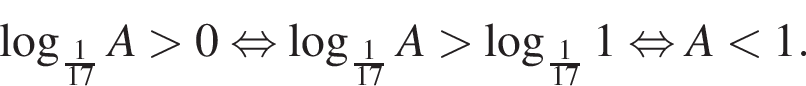
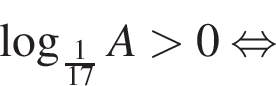
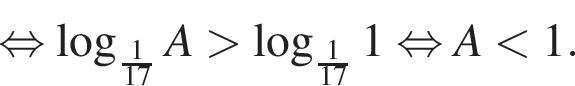

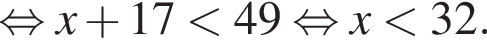

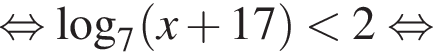
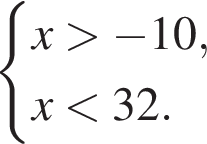 Поэтому наибольшее целое значение — 31, наименьшее целое значение −9, их сумма равна 22.
Поэтому наибольшее целое значение — 31, наименьшее целое значение −9, их сумма равна 22.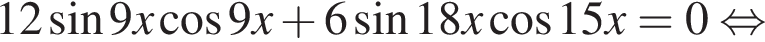
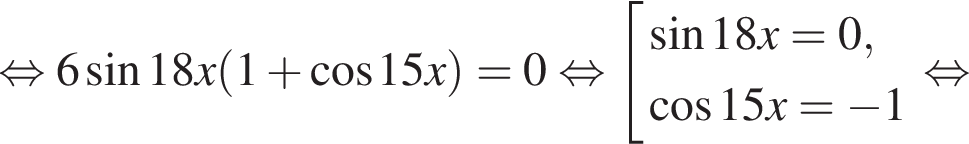
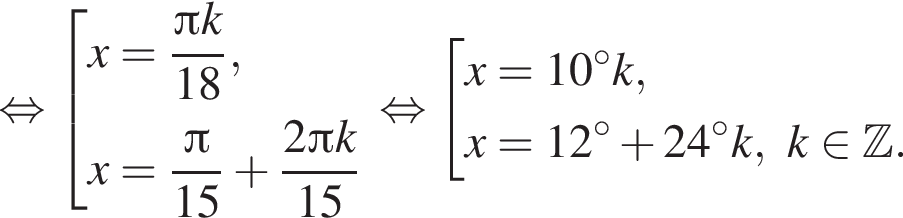
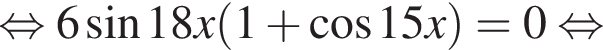
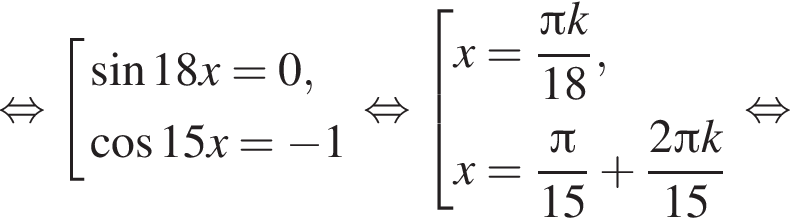
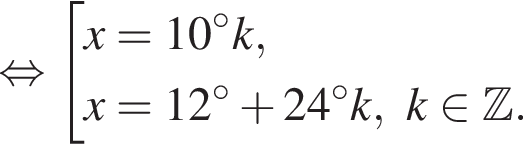
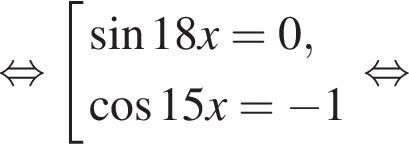
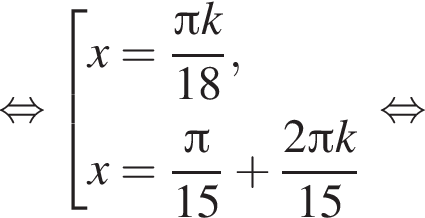
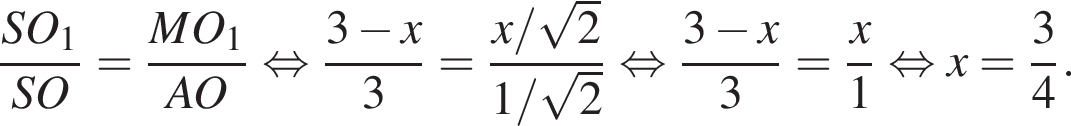
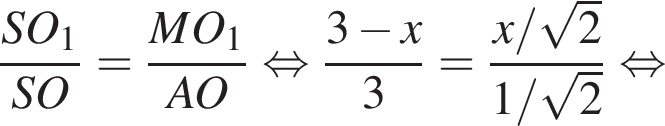
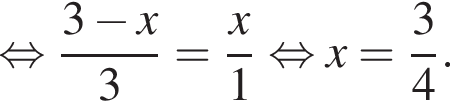
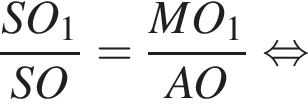
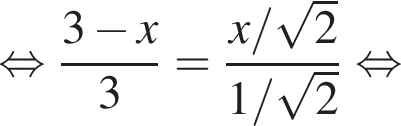
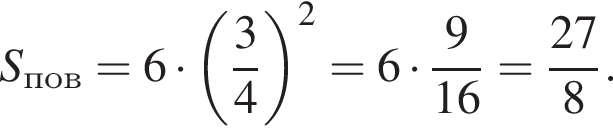
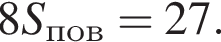
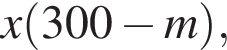 во втором —
во втором — 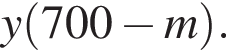 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 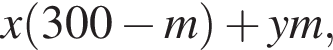 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 3:7. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 3:7. Тогда:


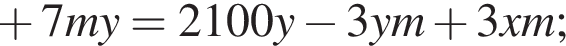
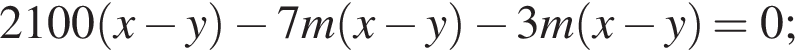
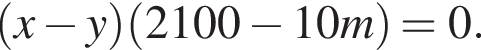

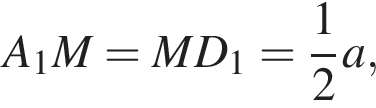
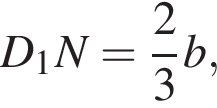
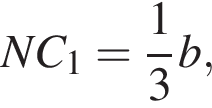
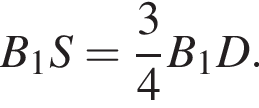
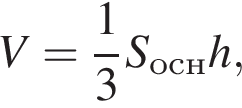 где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на втором рисунке.
где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на втором рисунке.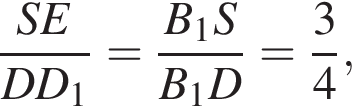 поэтому
поэтому 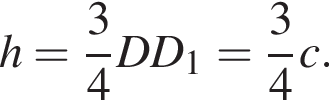



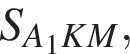 для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1 (см. рис. 3). Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому:
для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1 (см. рис. 3). Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому: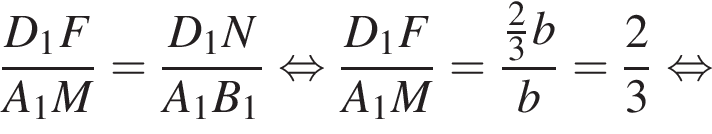
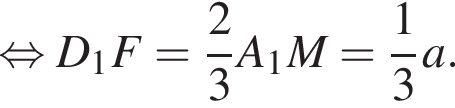

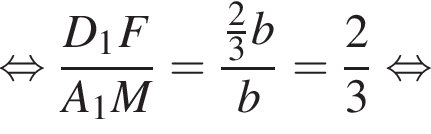
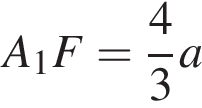 и
и 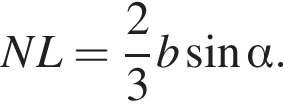 Соответственно, площадь треугольника A1NF равна
Соответственно, площадь треугольника A1NF равна